EVAP 3

CÁLCULOS SOBRE RESISTENCIA - CAMPO ELECTRICO – CAPACITANCIA Y VOLTAJE  EN  SERIES

 INTRODUCCION:

La electricidad en nuestra vida diaria

a electricidad influye notablemente en nuestra vida. Hay pocos momentos en que cada uno de nosotros no recurra a la electricidad para desarrollar una vida más fácil y cómoda.

Podemos pensar, por ejemplo, en lo distinto que sería la vida actual si no existiera luz eléctrica. Este quizá sea su mayor beneficio, pues gracias a ella la humanidad ha surgido de las tinieblas, incluso interiores, despejando numerosos miedos y reduciendo a una mínima expresión las leyendas y creencias nacidas del temor a la oscuridad. Reflexionemos sin embargo acerca de las demás cosas materiales que poseemos.

MARCO TEÓRICO

RESISTENCIA

Sabemos que una corriente eléctrica es un flujo de electrones. Al moverse a través de un conductor, los electrones deben vencer una resistencia; en los conductores metálicos, esta resistencia proviene de las colisiones entre los electrones. Si el paso es expedito y fluido los electrones viajarán ordenadamente, tendrán poca resistencia. Por el contrario, si el camino es muy estrecho o demasiado largo, los electrones se agolparán y chocarán entre sí, produciendo, además, mucho calor; se les opone una alta resistencia.

A. En un buen conductor, que opone baja resistencia, los electrones fluyen ordenadamente, sin chocar entre sí. B. En un mal conductor. eléctrico, que ofrece alta resistencia al flujo de corriente, los electrones chocan unos contra otros al no poder circular libremente y  generan calor, lo que aumenta la resistencia.

Entonces:

Se llama resistencia eléctrica a la oposición o dificultad que encuentra una corriente al recorrer un circuito eléctrico cerrado, y que permite frenar o atenuar el libre flujo de electrones.

La unidad de resistencia es el ohmio (W o Ω): y ohmio es la resistencia que ofrece un conductor cuando por él circula un amperio (intensidad)  y entre sus extremos hay una diferencia de potencial (tensión) de un voltio.

Físicamente, cualquier dispositivo o material intercalado en un circuito eléctrico representa en sí una resistencia para la circulación de la corriente eléctrica, y dependiendo de las características de dicho dispositivo o material se puede aumentar o disminuir la resistencia a una corriente eléctrica.

Por lo tanto, la resistencia eléctrica de un conductor depende de la naturaleza del material, de su longitud y de su sección, además de la temperatura.

A mayor longitud, mayor resistencia. A  mayor sección, menos resistencia. A mayor temperatura, mayor resistencia.

Para calcular el valor de la resistencia que ofrece un material específico, con largo y grosor definidos,  se aplica a fórmula

Léase: Resistencia ( R )  es igual al producto de rho (ρ) por la longitud (L) del conductor dividido o partido por la sección o grosor (área)  (S) del conductor.

Donde ρ (rho) es una constante (conocida y que depende del material), llamada resistividad.

L, es el largo o longitud (en metros) del cable o conductor, y S, es la sección o grosor (en mm²) del cable o conductor

CAMPO MAGNETICO

Consideremos una carga Q fija en una determinada posición y algunos puntos del espacio que rodean la carga. Si en cualquiera de esos puntos colocamos una carga q positiva que llamaremos carga de prueba, sobre ella actuaría una fuerza eléctrica ejercida por Q. Esto Indica que el espacio que rodea a Q se ha visto afectado por su presencia. Para describir este hecho se dice que Q genera un campo eléctrico a su alrededor y dicho campo ejerce una fuerza eléctrica sobre q

En un punto del espacio existe un campo eléctrico si al colocar una carga en dicho punto, actúa  sobre ella una fuerza  de origen eléctrico.

Es una magnitud vectorial, lo que implica que para  definirlo es necesario conocer su módulo, dirección y sentido en cada punto.

El vector campo eléctrico (E) creado por una carga Q, tendrá las siguientes características:

Dirección y sentido igual a la fuerza eléctrica que este campo aplicaría a una carga puntual q ubicado en dicho punto.

E = F / q

Consideraciones a tener en cuenta:

El campo eléctrico no depende de la carga de prueba q, sino de las cargas Q que lo producen.

Si la carga de prueba q fuera negativa, el sentido del campo eléctrico y la fuerza serian opuestos.

La unidad del campo eléctrico en el S.I. es N/C.

Capacitancia

Se define como la razón entre la magnitud de la carga de cualquiera de los conductores y la magnitud de la diferencia de potencial entre ellos.

La capacitancia siempre es una cantidad positiva y puesto que la diferencia de potencial aumenta a medida que la carga almacenada se incrementa, la proporción Q / V es constante para un capacitor dado. En consecuencia la capacitancia de un dispositivo es una medida de su capacidad para almacenar carga y energía potencial eléctrica.

La capacitancia tiene la unidad del SI coulomb por volt. La unidad de capacitancia del SI es el farad (F), en honor a Michael Faraday.

CAPACITANCIA = 1F = 1 C

El farad es una unidad de capacitancia muy grande. En la práctica los dispositivos comunes tienen capacitancia que varían de microfarads a picofarads.

La capacitancia de un dispositivo depende entre otras cosas del arreglo geométrico de los conductores.

Cuando un conductor se carga, es decir, se le comunica una carga eléctrica, adquiere un cierto potencial, que depende de consideraciones geométricas (de su forma). Pues bien;  
a la relación entre carga y potencial se le llama CAPACIDAD  de ese conductor.

 Podemos entonces definir una magnitud llamada CAPACITANCIA o CAPACIDAD, como la relación entre la carga almacenada (Q) y la tensión a la que se encuentra (V).

Escribimos entonces:

C = Q / V

CAPACITORES FIJOS

Estos capacitores tienen una capacidad fija determinada por el fabricante y su valor no se puede modificar. Sus características dependen principalmente del tipo de dieléctrico utilizado, de tal forma que los nombres de los diversos tipos se corresponden con los nombres del dieléctrico usado.

De esta forma podemos distinguir los siguientes tipos:

• Cerámicos.
• Plástico.
• Mica.
• Electrolíticos.
• De doble capa eléctrica.

VOLTAJE EN SERIE

CONEXION EN SERIE:

Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente. El esquema de conexión de resistencias en serie se muestra así:

Resistencias conectadas en serie

3.2.2. CONEXIÓN PARALELO:

Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, UAB, todas la resistencias tienen la misma caída de tensión, UAB. Una conexión en paralelo se muestra de la siguiente manera:

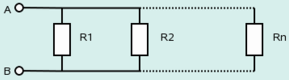
Resistencias conectadas en paralelo

3.2.3. CONEXIÓN SERIE PARALELO:

En una conexión serie paralelo se pueden encontrar conjuntos de resistencias en serie con conjuntos de resistencias en paralelo, como se muestra a continuación:

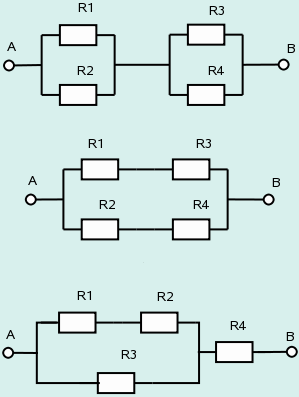
Resistencias conectadas en serie paralelo

3.3. RESISTENCIAS EN SERIE Y DIVISOR DE VOLTAJE:

El divisor de voltaje es una herramienta fundamental utilizada cuando se desean conocer voltajes de resistencias específicas, cuando se conoce el voltaje total que hay en dos resistencias. Es necesario considerar que el divisor de voltaje funciona para analizar dos resistencias, y que si se quieren determinar voltajes de más de dos resistencias utilizando el divisor de voltaje, deberá hacerse sumando resistencias aplicando paso a paso el divisor de voltaje de dos en dos, hasta llegar al número total de resistencias. Esto es muy útil porque en muchas ocasiones no es posible aplicar la Ley de Ohm debido a que sólo se tiene el valor de las resistencias, pero no se conoce el voltaje. Es entonces que se aplica el divisor de voltaje, con las siguientes fórmulas y de acuerdo al esquema mostrado a continuación:

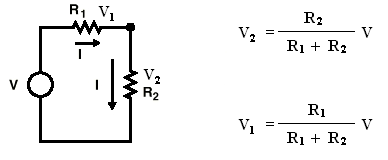
Otra herramienta importante es el divisor de corriente, que funciona para resistencias en paralelo. Sin embargo no fue necesario utilizarla en esta práctica, pues fue en las conexiones en paralelo ya se tenían los voltajes (que eran el mismo de la fuente por tratarse de conexión en paralelo) y los valores de las resistencias, por lo que las corrientes se encontraron fácilmente a través de la Ley de Ohm.

formula de cada problema de electricidad

#include <iostream>

#include <math.h>

using namespace std;

int main()

{

    // 1) DECLARACION

    // 2) ASIGNACION

    // 3) PROCESO

    // 4) RESULTADO 

 int opcion;

    cout<<"************ MENU PRINCIPAL ********** \n";

    cout<<"     1)FUERZA RESISTENCIA \n";

    cout<<"     2)FUERZA CAMPO MAGNETICO \n";

    cout<<"     3)FUERZA CAPACITANCIA \n";

    cout<<"     4)FUERZA VOLTAJE EN SERIE \n";

    cout<<"******************** \n";

    cout<<" INGRESE UNA OPCION: "; cin>>opcion;

    switch (opcion)

{

     case 1:

{

    cout<<"****** RESISTENCIA ****** \n\n";     

    int P, L, S;

    float Resist;

    cout<<"INGRESE SU CONSTANTE = "; cin>>P;

    cout<<"INTRODUZCA LA LONGITUD DEL CABLE(metro) = "; cin>>L;

    cout<<"INTRODUZCA EL AREA DEL GROSOR DEL CONDUCTOR = "; cin>>S;

    Resist =(P*L)/S;

    cout<<"LA RESISTENCIA ES = "<<Resist<<endl;

    cout<<" \n";

    cout<<" ********** \n";

    cout<<" \n";

}

break;

      

     case 2 :

{

    cout<<"****** CAMPO MAGNETICO ****** \n\n";     

    int q, v, betha;

    float CM;

    cout<<"INGRESE SU CARGA q = ";cin>>q;

    cout<<"INTRODUZCA LA velocidad v) = ";cin>>v;

    cout<<"INTRODUZCA EL FLUJO MAGNETICO = ";cin>>betha;

    CM = q * v * betha;

    cout<<"EL CAMPO MAGNETICO ES = "<<CM<<endl;

    cout<<" \n";

    cout<<" ********** \n";

    cout<<" \n";

}

break;

     case 3 :

{

    cout<<"****** CAPACITANCIA ****** \n\n";     

    int q, T;

    float CAP;

    cout<<"INGRESE SU CARGA ALMACENADA = ";cin>>q;

    cout<<"INTRODUZCA LA TENSION = ";cin>>T;

    CAP = q / T;

    cout<<"LA CAPACITANCIA ES = "<<CAP<<endl;

    cout<<" \n";

    cout<<" ********** \n";

    cout<<" \n";

}

break;

     case 4 :

{

    cout<<"****** VOLTAJE EN SERIE ****** \n\n";     

    int vo, v1, v2, r1, r2;

    float CAP;

    cout<<"INGRESE SU VOLATAJE = ";cin>>vo;

    cout<<"INGRESE SU VOLATAJE1 = ";cin>>v1;

    cout<<"INGRESE SU VOLATAJE2 = ";cin>>v2;

    cout<<"INGRESE LA r1 = "; cin>>r1;

    cout<<"INGRESE LA r2 = "; cin>>r2;

    v1 = (r1/r1 + r2)*vo ;

    v2 = (r2/r1 + r2)*vo ;

    cout<<"EL VOLTAJE1 EN SERIE ES :" <<v1<<endl;

    cout<<"EL VOLTAJE2 EN SERIE ES :" <<v2<<endl;

    cout<<" \n";

    cout<<" ********** \n";

    cout<<" \n";

}

break;

    cout<<endl; cout<<"\n";

    system("PAUSE");

    return 0;

} // FIN DEL PROGRAMA